Peter Shor Broke PKI with Ancient Math, and Futuristic Quantum Computing – Source: securityboulevard.com

Peter Shor revolutionized public-key infrastructure (PKI) using concepts that trace back to 4,000-year-old Babylonian mathematics and culminated in futuristic quantum computing. Here, we explore the math with a simple, illustrative tool to break PKI by hand.

The Theme: Simple Math Meets Cybersecurity

This blog delves into the math behind (breaking) cryptography, aligning with the theme of applying simple math to real-world cybersecurity. From the Babylonians, Euclid, Fermat, Euler, Fourier, and finally to Peter Shor, this journey underscores how ancient and modern mathematics, along with quantum computing, converge to break cryptography.

This blog is inspired by my amazing friend Ajit Hatti’s mandate to present in the cryptographic corner of the Data Security Council of India, Annual Information Security Summit. It was an extremely humbling experience as an amateur enthusiast to present in front of some of the most renowned professional cryptographers. The presentation focused on leveraging Shor’s algorithm to break PKI. You can explore the tool and presentation here: https://github.com/satyamtyagi/Shor-Excel.

Coincidentally, Google’s recent quantum computing milestone, #Willow, is remarkably relevant to this discussion. Ajit and I also discussed the implications of this announcement in a podcast with EXPLIoT founder Aseem Jaffer, available here: https://youtu.be/eMmD6U3E8ag?si=9Wt7o2ZoA-AZ5wqx

Building Towards Shor’s Algorithm

We’ll build towards Shor’s algorithm by exploring:

1. Euclid’s GCD algorithm
2. Babylonian quadratic solutions
3. Fermat and Euler’s theorems
4. Shor’s Algorithm
5. Quantum speedup
6. Quantum Fourier Transform and Continued Fractions

Altogether they may look intimidating, but we will explore them in small doses with simple examples.

2500-Year-Old Math: Euclid’s GCD algorithm

The father of geometry Euclid devised an efficient method to compute the Greatest Common Divisor (GCD). Here’s how:

• Divide the larger number by the smaller number.
• If the remainder is 0, the smaller number is the GCD.
• Otherwise, repeat with the smaller number and the remainder.

Example: GCD of 504 and 588

• 588 / 504 = 1 remainder 84
• 504 / 84 = 6 remainder 0
• GCD = 84

This method is efficient even for large numbers, with complexity O(b²), where b is the number of bits in the numbers.

Comparison: Normal Factorization for 504 and 588

To factorize both numbers:

• Factors of 504: 2 × 2 × 2 × 3 × 3 × 7
• Factors of 588: 2 × 2 × 3 × 7 × 7
• Common factors: 2 × 2 × 3 × 7
• GCD = 84

While factorization involves identifying and comparing all factors, Euclid’s algorithm skips this exhaustive process and directly computes the GCD efficiently.

Babylonian Algebra and its Connection to Modern Cryptography

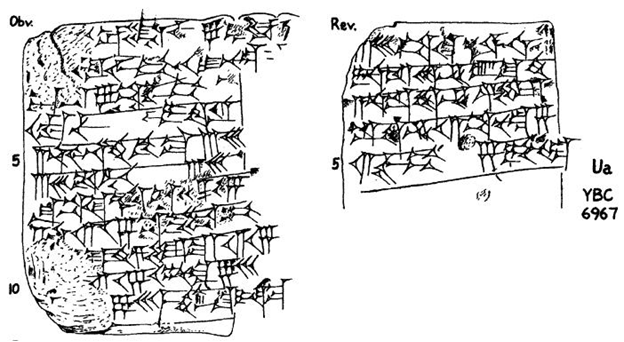
Over 4,000 years ago, Babylonian mathematicians demonstrated remarkable problem-solving skills, as evidenced by a clay tablet describing the solution to the equation:

x = 7 + 60/x

While their method may seem mysterious at first, it reflects an intuitive understanding of algebraic identities that form the foundation of solving quadratic equations. Let’s break down their steps and uncover the algebraic principles behind them.

Babylonian Method: Solving the Equation

The tablet outlines the following process:

1. Halve 7 to get 3.5.
2. Square 3.5 to get 12.25.
3. Add 60 to get 72.2.
4. Extract the square root to get 8.5.
5. Subtract 3.5 from 8.5 to get 5.
6. Divide 60 by 5 to get x = 12.

At first glance, this sequence might seem like numerical wizardry. However, it cleverly applies algebraic identities that modern students encounter in middle school.

The Algebraic Insight

The Babylonians implicitly understood key algebraic identities, including the difference of squares:

1. (a + b)² = a² + b² + 2ab
2. (a − b)² = a² + b² − 2ab

By subtracting the second identity from the first, we arrive at:

(a + b)² − (a − b)² = 4ab

Dividing by 4 gives the Babylonian formula:

((a + b)/2)² − ((a – b)/2)² = ab

Applying the Babylonian Formula to Solve the Equation

In the equation x = 7 + 60/x, let’s substitute:

• a = x,
• b = 60/x,
• a – b =7,
• ab = 60

In the Babylonian formula:

((a + b)/2)² − ((a – b)/2)² = ab

((a + b)/2)² = ((a – b)/2)² + ab

Here’s how their steps fit into this formula:

1. Halve a – b = 7 to get 3.5 i.e., (a – b)/2 = 3.5.
2. Square 3.5 to get 12.25 i.e. ((a − b)/2)²
3. Add 60 (i.e., ab) to 12.25 to get 72.25 i.e. ((a − b)/2)² + ab (the RHS)
4. Extract the square root of 72.25 to get 8.5 i.e. (a + b)/2.
5. Subtract 3.5 from 8.5 to find b = 5 i.e. (a + b)/2 – (a – b)/2
6. Divide 60 by 5 to find a = x =12 i.e. ab/b

This demonstrates how the Babylonians used quadratic reasoning, even without the modern notation we use today.

Connection to Modern Algebra and Shor’s Algorithm

The Babylonian insight links directly to the difference of squares formula:

x² − y² = (x + y) × (x − y)

This formula is crucial in modern algebra and factorization. For example, in the context of Shor’s algorithm:

1. Let x² – 1 = (x + 1) × (x − 1)
2. If x² – 1 = m × N, and x + 1 ≠ N and x – 1 ≠ N, the factors of N are shared with x + 1and x − 1.
3. By computing GCD (N, x − 1) or GCD (N, x + 1), we can extract factors of N.

In simpler terms, if we find an x such that x² mod  N = 1, then x² − 1 is divisible by N, and this relationship reveals the factors of N.

Fermat’s Little Theorem and Euler’s Totient Theorem

Now we go to just a few hundred-year-old math to find such an x Fermat showed that if N is a prime and G is coprime to N, then: G^N⁻¹ mod N = 1. Euler extended this to non-primes, stating: G^Φ(N) mod N = 1, where Φ(N) counts integers coprime to N. Using these theorems, we can pick any G coprime to N for factorizing N. So we know If G and N are coprime we can find some power p of G, G^p mod N = 1

If p is even then substituting G^p/2 for x in x² mod N = 1

1. (G^p/2)² -1 mod N = 1
2. (G^p/2 + 1) × (G^p/2 – 1) = m × N
3. GCD (G^p/2 ± 1, N) are factors of N

Shor’s Algorithm in 1994 IEEE Symposium on Foundations of Computer Science

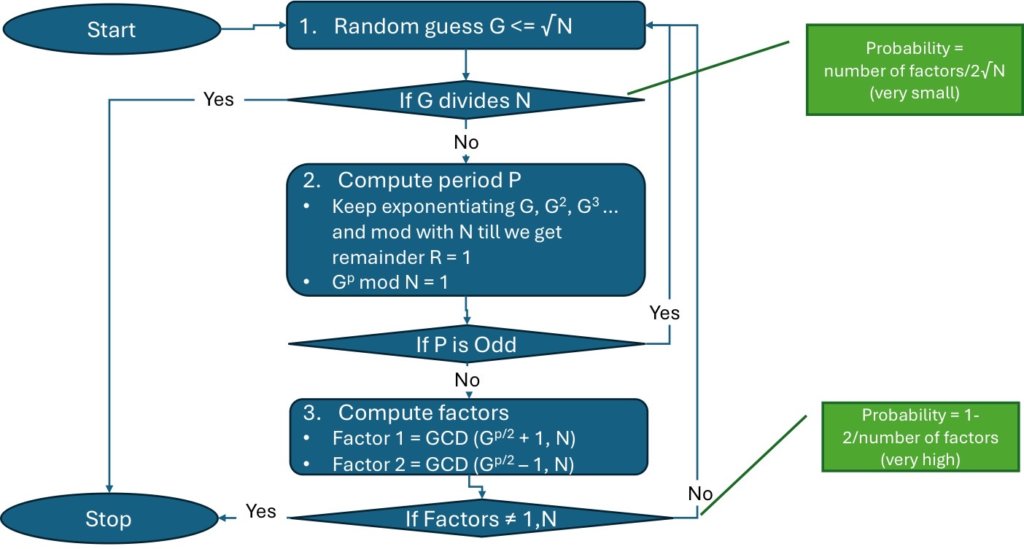
Just from the above math Shor built his algorithm

1. Random guess G £ ÖN
2. If G divides N, done we have factorized N
3. Otherwise compute period P such that G^p mod N = 1
4. If P is odd start over
5. Otherwise compute factors GCD (G^p/2 ± 1, N)
6. If factors are 1, N start over, otherwise done, we have factorized N

Example: Factorizing N = 35

1. Guess G = 2.
2. Compute 2^p mod 35:
3. 2¹ mod 35 = 2,
4. 2² mod 35 = 4, …,
5. 2¹² mod 35 = 1 (or P = 12)
6. Compute GCD (2^12/2 ± 1, 35)
7. GCD (65, 35) = 5
8. GCD (63, 35) = 7
9. Factors of 35 are 5, 7

You can try some examples and use the illustrative tool implemented in excel from here: https://github.com/satyamtyagi/Shor-Excel

Understanding Quantum Speed Up in Shor’s Algorithm

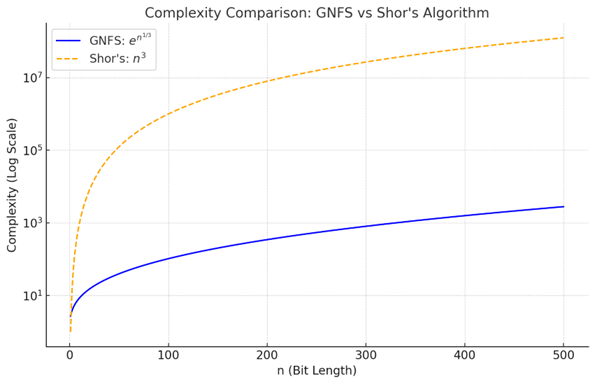
Quantum computing transforms the complexity of factorizing large numbers from O(2ᵇ) (exponential in the number of bits, b) to O(b³) (polynomial). This dramatic improvement is possible because quantum bits, or qubits, behave dramatically different from classical bits.

Classical vs. Quantum Bits: A Key Difference

• Classical bits can exist in one of two states, 0 or 1, at any given time.
• Quantum bits (qubits), however, leverage superposition to exist in a combination of 0 and 1 simultaneously.

This allows quantum computers to perform multiple calculations at once. To illustrate this:

Classical Bits Example:
Suppose you want to evaluate a function f(x) for two inputs x = 0 and x = 1. A classical computer would compute f(0) and f(1) sequentially, one after the other.

Quantum Bits Example:
Using a single qubit in superposition, a quantum computer can process both x = 0 and x = 1 simultaneously, effectively performing two calculations at once.

As the number of qubits increases, the quantum system can evaluate exponentially more possibilities in parallel, giving rise to its powerful speed-up.

To understand this speed-up, let’s start with a simple example:

Classical vs. Quantum Computation: A Toy Problem

Consider solving the equation x + 1 = 3 by testing all possible values of x. Here’s how it works on classical and quantum computers:

1. Classical 2-Bit Computer: A classical computer tests each value of x sequentially:
   • 00 + 1 = 01 (not 3)
   • 01 + 1 = 10 (not 3)
   • 10 + 1 = 11 (yes, 3!)

The answer is x = binary 10 (or decimal 2).

2. Quantum 2-Qubit Computer: A quantum computer, thanks to superposition, evaluates all possible values of xx simultaneously:
   • 00 + 1, 01 + 1, 10 + 1, 11 + 1 = 01, 10, 11, 00.

From this parallel computation, we extract x = binary 10 (or decimal 2). While this might not seem significant for small inputs, as the number of qubits grows, the quantum computer’s ability to handle all values at once results in exponential speed-up compared to a classical system.

Quantum Speed Up in Shor’s Algorithm: Factorizing Large Numbers

Applying quantum speed up to Shor’s algorithm, to factorize N = 35. Here’s how the steps compare:

1. Classical Approach: Compute the sequence 2^k mod  35 for k = 1, 2, 3, … sequentially:
   • 2¹ mod  35 = 2 mod 35 = 2
   • 2² mod  35 = 4 mod 35 = 4
   • 2³ mod  35 = 8 mod 35 = 8, and so on until 2^P mod  35 = 1 for P =12, the repeating cycle length.

2. Quantum Approach: The quantum computer evaluates all values of 2^k mod 35 simultaneously: 
   • 2¹ mod 35, 2² mod 35, …, 2¹² mod 35 = 2, 4, …, 1.

Instead of sequentially searching for P, quantum computers use quantum properties to compute all the results simultaneously.

Quantum computation holds all possible values in a superposition, but extracting the desired result (e.g., the period P) is non-trivial. This is where quantum interference comes into play: the algorithm amplifies the correct answer while suppressing incorrect ones, ensuring the output reflects P when measured.

Extracting the Period with Quantum Fourier Transform (QFT) and Continued Fractions

The Fourier Transform, introduced by Joseph Fourier, is a mathematical tool used to analyze periodic functions. It decomposes a complex waveform into its constituent frequencies. For instance, when you strum a guitar chord, the sound wave is a combination of frequencies from all the strings. The Fourier Transform can isolate these individual frequencies, revealing the notes being played.

In quantum computing, we use a similar technique called the Quantum Fourier Transform (QFT). However, instead of working with classical data, QFT operates on quantum states that encode many possibilities simultaneously (superposition). This makes it a critical step in Shor’s algorithm for finding the period (P). As not only G^p mod N = 1, But also G^x+p mod N = G^x , The (P) is the period of the function G^x mod N.

The challenge in quantum factorization lies in extracting the period P of the function f(x) = G^x mod N. Here’s how QFT helps:

1. Superposition: First, the quantum computer prepares a superposition of all possible values of x, which are the inputs to the function f(x) = G^x mod  N.
2. Interference from f(x): The function f(x) is applied to this superposition, creating a quantum state where the periodicity of f(x) is encoded in the phases of the quantum amplitudes.
3. Extracting Periodicity with QFT:
   • QFT transforms this quantum state into one where the dominant peaks (high probabilities) correspond to multiples of the frequency of the periodic function f(x).
   • These frequencies are directly related to the period P. The output of QFT gives an approximation of j/P, where j is an integer and P is the period.

In essence, QFT condenses the periodicity information hidden in the quantum state into a readable format, allowing us to extract P.

Using Continued Fractions to Compute P

The output of QFT provides k, and k/2ⁿ where n is the number of qubits provides a fractional approximation of j/P, i.e. k/2ⁿ = j/P where:

• k is the measured output from quantum computation
• 2ⁿ is the size of the quantum state (determined by the number of qubits n).
• j and P are integers, and P is the desired period.

To compute P, we convert k/2ⁿ into its simplest fractional form using continued fractions. Let’s work through an example:

Once QFT provides an approximation of the frequency, we use continued fractions to compute P. This ancient technique, even known to the Babylonians, refines the fractional approximation into its simplest form.

Let’s walk through an example:

1. Setup:
   • N = 15 (the number to factorize)
   • G = 7 (a randomly chosen co-prime)
   • k = 6 (measured output after quantum computation),
   • n = 3 qubits (so 2ⁿ = 8)

2. Compute k/2ⁿ:
   • k/2ⁿ = 6/8 = 0.75 This represents j/P, where j and P are integers.

3. Apply Continued Fractions:
   • Decompose 0.75 into its continued fraction representation:
     • a = 0 (integer part of 0.75).
     • a′ = 1 (integer part of 1/0.75 = 1.33).
     • a′′ = 3 (integer part of 1/0.33=31/0.33 = 31/0.33=3).
   • The continued fraction expansion of j/P is
     • j/P = a + 1/(a′+ 1/(a′′+…)) = 0 + 1/(1 + 1/3) = 3/4​.
4. Verify the Period P:
   • From j/P =3/4, we deduce P = 4.
   • Validate P using G^P mod N:
     • 7⁴ mod  15 = 2401 mod  15 = 1.

5. Factorize NNN:
   • Compute the greatest common divisors (GCDs) to find the factors:
     • GCD (G^P/2 − 1, N) = GCD (7² – 1, 15) = GCD (48, 15) = 3
     • GCD (G^P/2 + 1, N) = GCD (7² + 1, 15) = GCD (50, 15) = 5

Thus, the factors of N = 15 are 3 and 5.

This process elegantly combines QFT and continued fractions to extract the period of our function G^x mod N needed for factorization. QFT extracts periodic information, while continued fractions convert it into a usable form.

Summary and Future of Cryptography with Quantum Computing

Mathematical Insights and Quantum Innovation Challenge PKI

Public Key Infrastructure (PKI) and RSA encryption rely on the assumption that factorizing large numbers is computationally infeasible for classical computers, ensuring the security of modern communication.

Quantum computers, leveraging Shor’s algorithm, can disrupt this security paradigm by making factorization exponentially faster using clever mathematical insights and quantum principles.

Exciting Future: Breaking and Reinventing Cryptography

While advancements in quantum hardware, like Google’s #Willow achieving over 100 physical qubits, are impressive, the number of logical qubits—error-corrected and usable qubits—remains limited. It will still take time to build systems powerful enough to break RSA in practice.

One startling update comes from Australia, which has outlined plans to transition its cryptographic systems to post-quantum standards by 2030, as noted in recent guidance from the Australian Cyber Security Centre. This is partly because a quantum-based attack, derived from Shor’s algorithm, can undermine virtually all conventional asymmetric cryptography—spanning RSA, Diffie-Hellman, ECDH, and ECDSA—once a sufficiently powerful quantum computer emerges. Although such a machine does not yet exist, the rapid progress in quantum technology indicates these older methods will eventually need to be replaced. Consequently, any new cryptographic tools intended for use beyond 2030 should align with post-quantum cryptographic standards approved by security authorities, ensuring long-term protection against future quantum threats.

In response, mathematicians and cryptographers are actively developing quantum-resistant algorithms, such as lattice-based cryptography, to secure systems against future quantum attacks.

I am hopeful that the mathematical beauty behind quantum computing, and cryptography inspires others as it inspires me. By exploring these ideas, we can drive breakthroughs uncovering innovative ways to break cryptography and, in the process, create even stronger cryptography.

The post Peter Shor Broke PKI with Ancient Math, and Futuristic Quantum Computing appeared first on ColorTokens.

*** This is a Security Bloggers Network syndicated blog from ColorTokens authored by Satyam Tyagi. Read the original post at: https://colortokens.com/blogs/quantum-computing-cybersecurity/