OMEN Improvements – Source: securityboulevard.com

August 10, 2025
Post Author / Publisher: Security Boulevard

CISO2CISO post categories: Cyber Security News, rss-feed-post-generator-echo, Security Bloggers Network, Security Boulevard

Rate this post

Source: securityboulevard.com – Author: Matt Weir

“If I had an hour to solve a problem, I would spend 55 minutes thinking about the problem and five minutes finding the solution.”

– Albert Einstein

Introduction:

I’m a big fan of graphing password cracking sessions. It’s a good way to figure out what’s working and what isn’t by highlighting trends that get lost in the final “cracking success” number. The very first thing I look for in these graphs is saw-tooth steps. This is an easy way to spot potential improvements. If you suddenly see a quick run of cracks in your password cracking success rate, which is what these saw-tooth steps represent, that implies you can optimize your cracking session by moving that attack earlier in your workflow. Now you need to temper that with the realization that no two password sets are exactly the same, you don’t want to overtrain your cracking sessions on one particular dataset, and often these improvements come about because you learn some target specific information part-way through your cracking session. But all that being said, these saw-tooth steps are a great place to start your investigations.

These saw-tooth steps are very evident in the current OMEN cracking sessions as you can see in the graph below. This post will cover my investigation into making OMEN better based on these observations. But if you take anything away from this post, it’s really that you should graph your cracking sessions, (ideally using a linear and not logarithmic scale), as chances are it will help you optimize your cracking techniques as well.

OMEN Background:

At a high level OMEN is simply another Markov based password guess generator. What makes it stand out from other Markov approaches though is in how it calculates probability thresholds for generating guesses. Rather than ordering likely “next characters” in an array or queue and selecting the next most likely option (such as Hashcat’s Markov or “roughly” like JtR’s Incremental), or multiplying probabilities together and using a probability threshold (like JtR’s –Markov option), OMEN instead assigns each transition a “cost” between 0-10, and then allocates a total “guessing budget” for generating guesses based on the current “level” it is at. So for an OMEN level 4 guess, it would have a “budget” of 4 it needs to spend on all the transitions when creating a guess. The nice thing about this is that when calculating an OMEN guess, you only need to do integer addition. This is a huge bonus from a speed perspective since multiplying floats (like JtR’s Markov) is expensive. This approach also gives you much more granular control about the different probability costs associated with a transition compared to using an array based ranking which is what Hashcat does.

The key thing to keep in mind are there are 4 items that OMEN can spend its budget on, of which 3 are currently in use:

Initial Probability (IP): This is the first N-1 characters to start a password guess with.

If you have a NGram length of 4, this is the first 3 characters of your password guess.
The IP is trained from the start of all passwords in the training set
Because the IP isn’t trained on the full password, there tends to be a lot of gaps. For example, when trained on a 1 million subset of RockYou with the default alphabet of 72 characters, the total keyspace would be around 373k lines, but the OMEN IP list only contains roughly 90k lines.

Length (LN): The total length of the password guess

OMEN prioritizes guesses based on their length so if a password guess has a “non-standard” length it is penalized with a higher cost.
The reason I want to highlight this is because **Spoiler** this is where some of the improvements can be made in the standard OMEN algorithm.

Conditional Probability (CP): This is the likelihood of the “next” character appearing.

For example if the previous three characters are “que”, the CP cost of the next letter being ‘[e,s]’ might be 0, and the next letters being ‘[a,n]’ might have a CP cost of 1.

End Probability (EP) (NOT USED): The probability of the last couple of characters in a password

Note: Neither the Rub-SysSec or Py-OMEN currently use EP even though both the tools still calculate it. This is because testing revealed using EP makes the guesses significantly worse. I know that sounds counter-intuitive, but that’s why we run tests!

OMEN Investigation:

To better investigate and OMEN attacks, there are three repos I’ll be using:

Py-OMEN: A python implementation of the Rub-SysSec OMEN attack

Link: https://github.com/lakiw/py_omen
Comments: I’ve been fixing this up so it actually works. This is the same algorithm as the OMEN implementation in the PCFG toolset but it is standalone without any of the other PCFG code. So if you are running real cracking sessions I’d still recommend using the PCFG toolset instead, but this standalone version is easier to work with when investigating improvements to OMEN.

Password Research Tools: Allows graphing and investigating the effectiveness of password attacks.

Link: https://github.com/lakiw/Password_Research_Tools
Comments: After many years, I’m also updating this toolset to add a few more features. Specifically I can send it debug statements from my guess generator and it’ll include when in the guessing process the statement was outputted. This is helpful for investigating when OMEN levels change. All graphs here are generated using that tool + Excel.

Pretty Cool Fuzzy Guesser (PCFG): My main password guess generating toolset.

Link: https://github.com/lakiw/pcfg_cracker
Comments: Hey, if I’m going to make an improvement in how guesses are generated, of course I’m going to use that to upgrade my main toolset!

The first thing I did when investigating the saw-tooths in OMEN attacks was to run a cracking session and save all the CRACKED passwords to file as well as collect data for my graphs. That way when I wanted to dig into a particular run of cracked passwords from looking at the graph I can see what those passwords are. An example cracking session can be seen as follows:

python3 enumNG.py -r mod_rockyou1 | python3 ../Password_Research_Tools/checkpass.py -m 1000000000 -t ../../research/password_lists/rockyou/rockyou_32.txt –cracked_file rockyou1_vs_rockyou32.cracked

Note: You can also do something similar with Hashcat giving it the flag “–outfile-format=2,4” which will output the plaintext password followed by the guess number. Another option to make parsing easier is to save the hex_plain vs. the raw plaintext using the flag “–outfile-format=3,4“. This can be annoying as it requires the extra step of decoding the plaintext password to do any manual analysis, but that’s often a lot less annoying than dealing with parsing issues.

Hashcat Feature Request: (NOTE: This may be outdated since the new version of Hashcat has a ton of improvements) It would be nice if Hashcat honored the ordering of the –output-format listing so I could put in “–outfile-format=4,2” and it would print the guess number first. Right now, it ignores the ordering and will put the plaintext password first if you use that command.

Moving on, one nice thing about using py-omen is it has a “test” mode which allows you to paste in strings and see how they would be parsed by OMEN. For example, this is me analyzing the cracked password “talishka”

Here you can see that a length 8 guess had a cost of 1. The initial IP “tal” had a cost of 2. The rest of the costs are from the transitions with the ISH->K being the big cost with a price of 3. The total level that this guess would be generated at would be 8 (aka 1 + 2 + 1+ 1+ 3).

I then put “break points” in my graph by having my OMEN implementation output a debug statement whenever it made a major transition (first when the level increased, and then when things like the IP or length changed). This allowed checkpass to note in a cracking session when those transitions occurred. This was super helpful since I could put dots on my graph and start to really understand what was happening when those sawtooth improvements kicked in.

Looking through the sawtooth portions of the graph for an attack using the RockYou1 training set and the RockYou32 test set, I noticed that the transitions and IP tended to be all over the place, but that the length costs were relatively low. Basically the OMEN guesser did really well when it spent its level price on anything BUT length. What this seemed to imply was that the cost for longer passwords was not being weighted in an optimal fashion. Or to put it another way, making longer guesses probably needed to be more costly.

So let’s test this out. As a totally non-scientific test to basically “muck around with the data to quickly test a hypothesis”, I manually modified the OMEN ruleset trained on the RockYou1 training data and increased the cost of any length that wasn’t already at a 0 cost by 1. So if the cost was 0 it stayed 0, but if the cost was 1, it was now 2. If it was 2, it was now 3. Etc. I then reran a test against the RockYou32 test set and then compared the results.

It’s not pretty, but it certainly represents an improvement. Now this is only one test against one dataset. And it was a short test at that. But as a first quick test the results were promising enough that it convinced me it was worth spending a bit more time refining the improvement before running longer and more diverse tests.

Increasing the Cost of OMEN Lengths:

At this point, my theory was that the cost of longer passwords was too low in the current OMEN implementation. In the default OMEN algorithm, the “Length Cost” is based on how likely passwords of that length are to be found in the training set. For example: If length 7 passwords are the most comment in the training set, then the OMEN “Length Cost” for 7 character passwords would be 0. Let’s assume though that length 6 and length 8 passwords showed up at relatively the same frequency in the training set. In this example, they might be frequent enough that they would be assigned an OMEN “Length Cost” of 1. This means the OMEN cost of generating a length 6 and 8 password would be the same, even though it seems like you’d have better success making a length 6 guess vs. a longer length 8 guess when using brute force techniques.

One area where the longer OMEN generated passwords might get more cost is that the “Conditional Probability” costs of adding extra letters may not be 0. But many of the high probability CP costs ARE zero, which means you can add as many as you want and they won’t increase the overall cost. This leaves us two options to make it so that in the above example length 8 guesses have a higher cost than length 6 guesses:

We can directly add additional cost to the “Length Cost” to make longer passwords more costly
We can remove 0 cost “Conditional Probability” transitions, so that way any added character is guaranteed to have a cost associated with it.

There’s plusses and minuses to both approaches. I wish I could say I weighed those out, ran multiple tests, and settled on a specific implementation, but I picked option #1 of adding an additional cost for each extra character to the “Length Cost” since it was the easiest to do. The new approach is described below:

Updated Length Cost Training Algorithm:

Calculate the length cost as in the base OMEN algorithm.

##–Calculate the probi values

probi = base_count / total_count

probi *= level_adjust_factor

probi += 0.00000000001

##–Now calculate the level

level = math.floor(–1 * math.log(probi))

Next add an additional cost of the length * (cost_factor) to each Length Cost. So if 6 character passwords had a starting cost of 2, and the cost_factor was 1, then the total cost would now be [2 + 6 x 1] which is 8.
Finally find the lowest length cost, and set that cost to 0, and reduce the cost of all the other length costs by the original amount of the lowest length cost. This was just because I like the OMEN algorithm to start at cost 0 so at least one length cost needed to be 0 to allow that.

OMEN Improvement Results:

For my next test, I used the updated Length Cost calculation, and assigned it a cost-factor of 1. Therefore each additional character added to an OMEN guess increased the cost of the guess by 1. This is in addition to the other weighting/cost factors so there is still a “base” extra cost for non-frequent lengths as well. Running the same test as above, with training on the RockYou1 dataset and testing against the RockYou32 set yielded the following results:

Picture of the OMEN Length Improvement doing better than the original algorithm

I’ll be up front, I was not expecting this much of an improvement. Now on a longer cracking session, I expect to two lines to converge more. This modification doesn’t impact the types of guesses OMEN generates. It just makes OMEN generate shorter guesses sooner. Still, cracking more passwords quickly is always a welcome change (from the perspective of the red team member that is).

But if we’re getting nitpicky, (and this whole post is evidence that I am), even in this new graph there still are sawtooth steps. They are much smaller, but they are still there. Let’s see then if modifying the length cost factor improves things even more. I wanted to check if a cost factor of 1 was either too high or too low, so I ran two more tests, one with a cost factor of 2 (so each additional character added 2 to the cost), and the other with a cost factor of 0.5 (where it would be rounded down to the nearest integer). Here are the results:

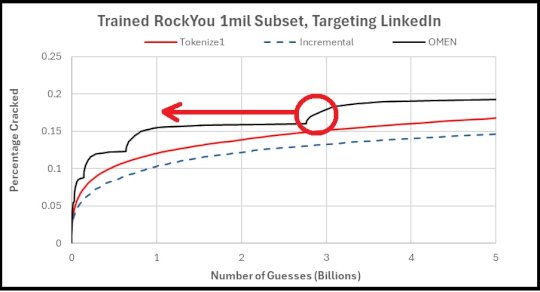
Giving OMEN a length cost factor of 1.0 worked the best, though 0.5 was close. This implies there’s still a lot of value of trying length 6/7/8 passwords vs. overly focusing on passwords length 5 and lower. Now this doesn’t answer the question about how to smooth out the remaining sawtooth steps, but this seems good enough for now. The next thing to do is to run this test on a different password dataset. For this test, I ran the base OMEN algorithm against an OMEN with a length cost factor of 1, both trained on Rockyou1 against the full list of cracked LinkedIn passwords.

Once again, the results point to a noticeable improvement. The LinkedIn set is a much tougher one to crack, as evidence by the significantly lower success rate, so seeing the modified OMEN attack do better against it is a good indicator that the modifications represent a real improvement vs. being a fluke.

Next, I was excited to see if I could fold these improvements into my PCFG toolset. The PCFG toolset also uses OMEN for its brute-force guess generation so it can create “words” not seen in the training set. Therefore I was able to copy paste the changes from py-OMEN into the PCFG code and train the OMEN portion using a length cost of 1. When I then ran a cracking session (trained on RockYou1) against the LinkedIn list using the “base” PCFG ruleset and the modified PCFG ruleset the following results were produced:

Breaking down these results, the base PCFG does better than the previously modified OMEN attack. That’s not surprising, since the PCFG guess generator uses a lot of mangling rules that make it hard for any pure-brute force attack to keep up with it, (at least for shorter cracking sessions). But by adding a length cost factor into the OMEN algorithm that the PCFG toolset uses, I was really impressed by how much more effective it made the PCFG attack.

This seems like a clear win, so I pushed these changes to the core PCFG toolset and they will be available starting with version 4.8 of the pcfg-trainer. I also updated the Default PCFG ruleset to include these changes. That way if you run a standard attack the changes will already be applied. If you are using a custom ruleset that you trained yourself, you’ll need to retrain that custom ruleset for the changes to take effect though.

The TLDR of this entire blog post is that the PCFG password cracker has gotten better. But as I said at the start of the blog post, I hope if you take anything away from this entry, it is the value of graphing out cracking sessions to understand what is going on. There is still a lot of room for improvement. Finding those improvements though really depends on someone going “huh, that looks weird” and digging into it.

The post OMEN Improvements appeared first on Security Boulevard.

Original Post URL: https://securityboulevard.com/2025/08/omen-improvements/?utm_source=rss&utm_medium=rss&utm_campaign=omen-improvements

Category & Tags: Security Bloggers Network – Security Bloggers Network